Research Interests

My research interests lie in the following broad areas:

  • Digital Communications
  • Information Theory
  • Data Compression
  • Coding Theory and Practice
  • Machine Learning
  • Circuit Design
  • Quantum Error Correction
  • Post-Quantum Cryptography

Dr. Mitchell received the National Science Foundation CAREER award in 2022, the National Science Foundation's most prestigious award in support of early-career faculty, and the 2019 NMSU Early Career Award for Exceptional Achievements in Creative Scholarly Activity. He has received three best paper awards and is the recipient of the 2019 New Mexico EPSCoR Mentor Award. He currently holds the IFT Professorship in Telecommunications at the New Mexico State University.

Current Research Projects

Previous Research Projects

Coded Discrete Variational Autoencoders (Coded-DVAEs)

The influence of generative artificial intelligence (genAI) on industries and everyday life has been transformative. Advanced models, such as large language models (LLMs), have revolutionized natural language processing, enabling sophisticated conversational agents for tasks ranging from customer service to personal assistance. Diffusion models (DMs) have enhanced generative art and image synthesis, enabling the creation of highly realistic images and artwork from text prompts. However, current AI systems often lack uncertainty calibration, since they are trained using maximum likelihood objectives. This is known to result in neural networks that tend to provide confidence levels in their predictions that do not align with their precision.

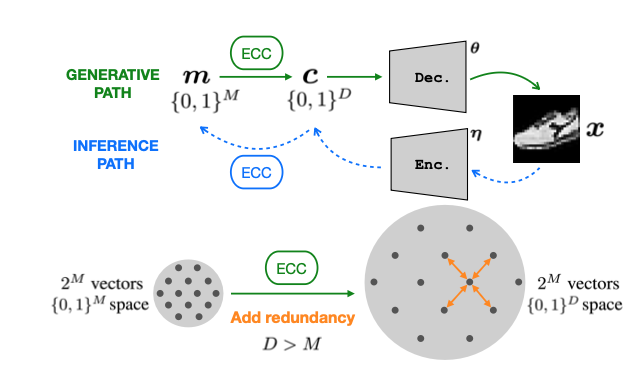
This project investigates a novel method to improve variational inference and representation learning in generative models with discrete latent variables. In particular, for a latent variable model, we argue that one should use error-correcting codes to introduce redundancy into the latent sample before the reconstruction decoder network processes it to generate the data (see upper figure). The variational approximation to the true posterior distribution can then exploit the added redundancy to provide more accurate estimates, reducing, in turn, the variational gap to the data likelihood. For different datasets, our results demonstrate that, compared to the uncoded DVAE, the coded-DVAE achieves superior generation quality (see figure on the right), better data reconstruction, and critically calibrated uncertainty in the latent space.

Selected publications:

  • M. Martínez-García, G. Villacrés, D. Mitchell, P. M. Olmos, "Improved Variational Inference in Discrete VAEs using Error Correcting Codes," Proc. Conference on Uncertainty in Artificial Intelligence, Rio de Janeiro, Brazil, July 2025.

Machine Learning Techniques for 6G Communication Systems

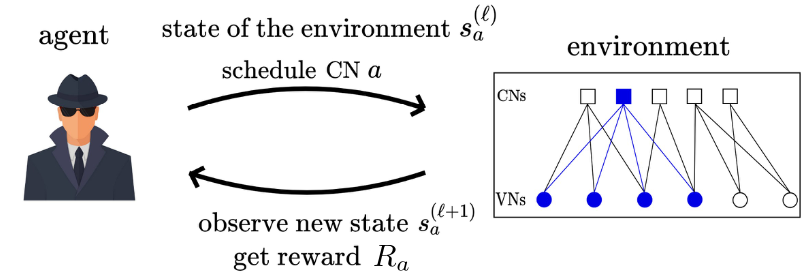Efficient forward error correction schemes are critical for ultra reliable low latency communications (URLLC) in sixth generation (6G) communications and beyond. However, the design of such codes for attaining both low error-floor and good decoding threshold is a challenging problem, particularly under stringent power consumption limitations. In this project, we leverage reinforcement learning (RL) to enhance sequential decoding of various candidate coding schemes proposed for 6G, including generalized low-density parity-check (GLDPC) and polar codes. Sequential decoding refers to the scheduling order of messages passed in the decoder iteration. The goal of RL is to determine an optimized scheduling policy (see figure on the right), i.e., one that results in a decoded codeword by minimizing the complexity of the belief propagation (BP) decoder. We show that the optimized schedule improves the convergence speed by 30-50% (significantly reducing decoder latency and power consumption) as well as improving the reliability.

In machine learning based Internet of Things (IoT) systems, data is captured by IoT devices and then transmitted over a wireless channel for remote processing. Since noise often appears on the channel, channel protection must be provided to guarantee an acceptable error rate, especially in safety-critical applications. In this project we propose a "joint learning and channel coding" (JLCC) scheme, where the ML model is retrained to tolerate some channel errors (figure on the right). Our results show that, when employing JLCC with the proposed retraining method, an average reduction of 29.15% and 34.82% in the dissipated power is achieved.

Selected publications:

  • M. Moradi*, S. Habib*, and D. G. M. Mitchell, "Enhancing Belief Propagation Decoding of Polar Codes: A Reinforcement Learning Approach," IEEE Communications Letters, vol. 29, no. 6, pp. 1285-1289, June 2025.
  • H. Hatami, D. G. M. Mitchell, D. J. Costello, Jr., and T. E. Fuja, "Threshold-based min-sum algorithm to lower the error floors of quantized low-density parity-check decoders," U.S. Patent No. 12,334,954 B1, issued June 17, 2025.
  • S. Habib* and D. G. M. Mitchell, "Reinforcement Learning for Sequential Decoding of Generalized LDPC Codes," Proc. International Symposium on Topics in Coding, pp. 1-5, Brest, France, Sept. 2023.
  • X. Tang, P. Reviriego, W. Tang, D. G. M. Mitchell, F. Lombardi, and S. Liu, “Joint Learning and Channel Coding for Error-Tolerant IoT Systems based on Machine Learning,” IEEE Transactions on Artificial Intelligence, vol. 5, no. 1, pp. 217-228, Jan. 2024.

Quantum Error Correction

Quantum computing has the potential to bring the second revolution in information technology as a result of the exponential computational speedup that is possible for certain problems. This technology will lead to systems vastly more powerful than today’s most powerful supercomputers. A serious obstacle to realizing the full potential of quantum computing lies in the decoherence of quantum states. Small amounts of noise create errors in qubit states that rapidly accumulate, making non-trivial computations impossible. Quantum error correction can address this but there are several significant challenges to overcome.

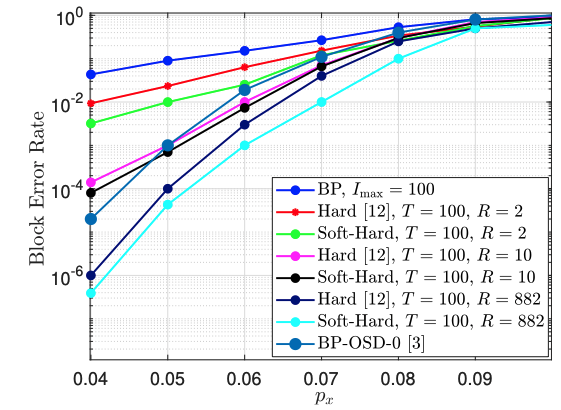
In this project we are currently pursuing two major directions: (1) design of good quantum LDPC (QLDPC) codes and quantum convolutional codes (QCCs) and (2) addressing the non-convergence of iterative decoders for quantum codes. In the first direction, we are leveraging graph theory and the design of orthogonal codes to maximize the sphere packing properties of pairs of convolutional codes. In the second direction, we are investigating proofs of decoding algorithm convergence using a technique called decimation - which progressively reduces the solution space of estimated bit and phase errors. The figure on the right shows that the proposed decimation technique, named "Soft-hard", can outperform state-of-the-art decoders for a range of bit flip probabilities p_x.

Selected publications:

  • V. Nourozi and D. G. M. Mitchell, "Quantum Convolutional Codes Constructed from Classical Self-Orthogonal Convolutional Codes," Proc. IEEE International Conference on Quantum Computing and Engineering, Albuquerque, NM, Sept. 2025.
  • M. Alinia, D. G. M. Mitchell, H. Yao, and H. D. Pfister, "Decimation Strategies for Belief Propagation Decoding of Quantum LDPC Codes," Proc. International Symposium on Topics in Coding, Los Angeles, CA, Aug. 2025.

Spatially Coupled LDPC (SC-LDPC) Codes

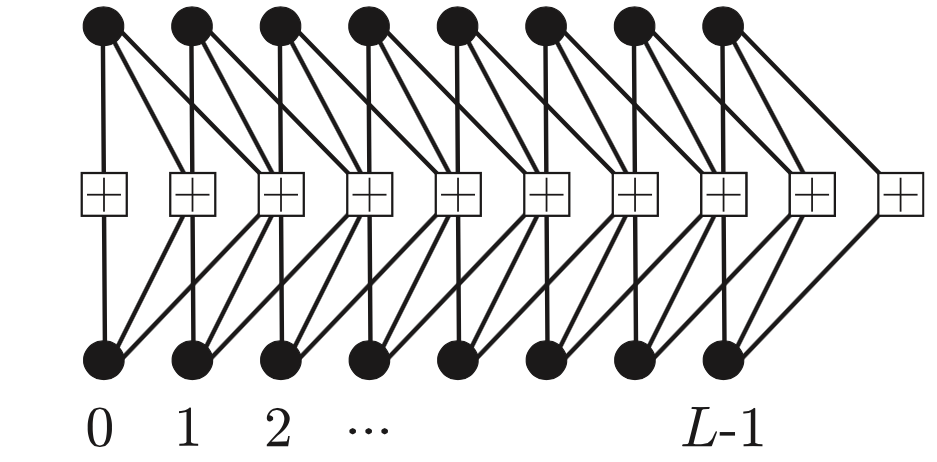Recently, iterative processing on spatially coupled sparse graphs has received a lot of attention in the literature. The concept of coupling a sequence of identical small structured graphs into a chain of length L with improved properties, first demonstrated in the context of low-density parity-check (LDPC) convolutional codes, has been shown to be applicable to a diverse list of topics, such as compressed sensing, multiuser communication, quantum codes, relay channels, wiretap channels, and models in statistical physics.

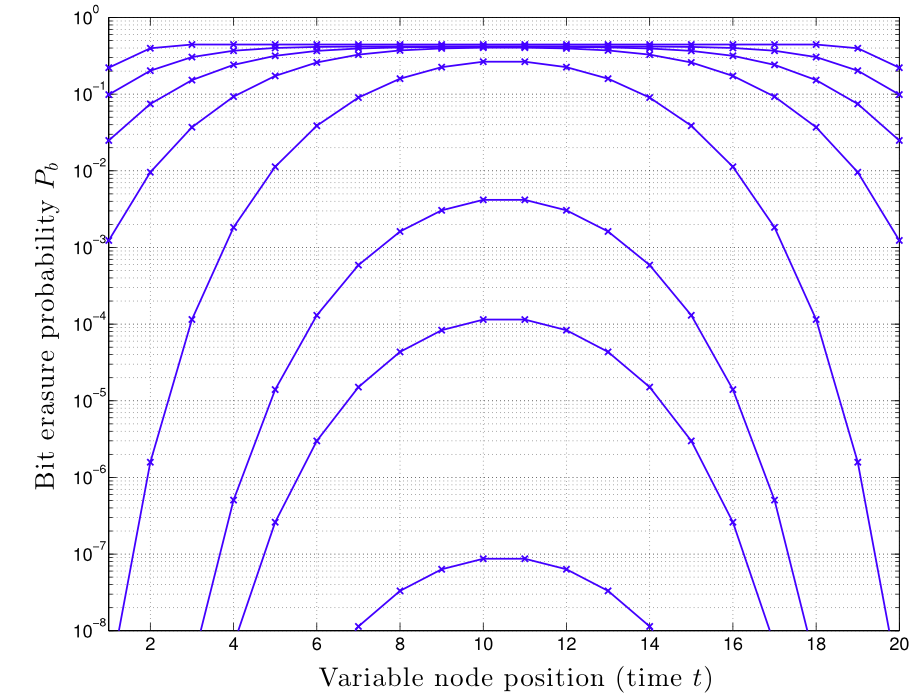In this project, we showed that SC-LDPC codes have a unique combination of capacity approaching thresholds and linear growth of minimum distance with constraint length, thereby promising excellent performance at low and high signal-to-noise ratios. The figure to the right shows the remarkable “wave-like decoding” characteristics of SC-LDPC codes - as we iterate the decoder (curves from top to bottom) the probability of error decays rapidly from the ends of the chain to the center.

Selected publications:

  • D. G. M. Mitchell, M. Lentmaier, and D. J. Costello, Jr., “Spatially Coupled LDPC Codes Constructed from Protographs,” IEEE Transactions on Information Theory, vol. 61, no. 9, pp. 4866-4889, Sep. 2015.
  • D. G. M. Mitchell, P. M. Olmos, M. Lentmaier, and D. J. Costello, Jr., “Generalized Spatially-Coupled LDPC Codes: Asymptotic Analysis and Finite Length Scaling,” IEEE Transactions on Information Theory, vol. 67, no. 6, pp. 3708-3723, June 2021.
  • M. Zhu, D. G. M. Mitchell, M. Lentmaier, and D. J. Costello, Jr., "Error Propagation Mitigation in Sliding Window Decoding of Spatially Coupled LDPC Codes," IEEE Journal on Selected Areas in Information Theory, vol. 4, pp. 470-486, 2023.
  • K. Huang, D. G. M. Mitchell, L. Wei, X. Ma, and D. J. Costello, Jr., “Performance Comparison of LDPC Block and Spatially Coupled Codes over GF(q),” IEEE Transactions on Communications, vol. 63, no. 3, pp. 592-604, Mar. 2015.
  • D. J. Costello, Jr., L. Dolecek, T. E. Fuja, J. Kliewer, D. G. M. Mitchell, and R. Smarandache, “Spatially Coupled Sparse Codes on Graphs - Theory and Practice,” IEEE Communications Magazine, vol. 52, no. 7, pp. 168-176, July 2014.
  • L. Wei, D. G. M. Mitchell, T. E. Fuja, and D. J. Costello, Jr., “Design of Spatially Coupled LDPC Codes Over GF(q) for Windowed Decoding,” IEEE Transactions on Information Theory, vol. 62, no. 9, pp. 4781-4800, Sept. 2016.

Lossy Source Coding

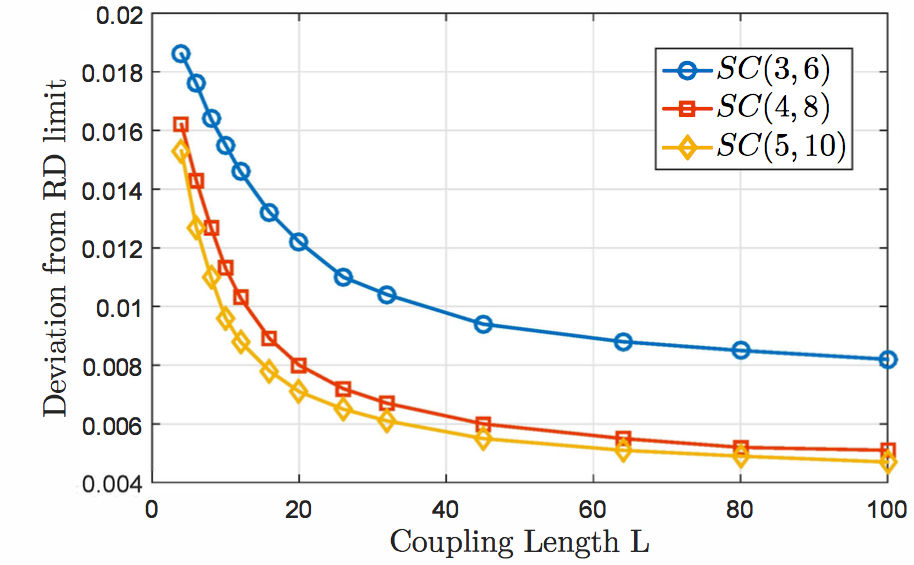Lossy coding of speech, high quality audio and video, and so on, is widespread today. Compared to lossless compression, where the source must be reconstructed identically from its compressed version, the lossy source compression problem requires the reconstructed data to be correct only up to some specified distortion measure. In this project, we investigate the distortion performance of a practical class of protograph-based, spatially coupled low density generator matrix (SC-LDGM) codes and show that they have distortion performance very close to the rate-distortion (RD) limit, as the “coupling length” L grows, with low-to-moderate encoding latency. We then extended the construction to show that concatenated SC-LDPC codes display a notable performance improvement compared to existing state-of-the-art joint source-channel coding schemes based on LDPC codes with comparable latency and complexity constraints.

Selected publications:

  • A. Golmohammadi* and D. G. M. Mitchell, “Concatenated Spatially Coupled LDPC Codes with Sliding Window Decoding for Joint Source-Channel Coding,” IEEE Transactions on Communications, vol. 70, no. 2, pp. 851-864, Feb. 2022.
  • A. Golmohammadi*, D. G. M. Mitchell, J. Kliewer, and Daniel J. Costello, Jr., "Encoding of Spatially Coupled LDGM Codes for Lossy Source Compression," IEEE Transactions on Communications, vol. 66, no. 11, pp. 5691-5703, Nov. 2018.
  • A. Golmohammadi, J. Kliewer, D. J. Costello, Jr., and D. G. M. Mitchell, “On the Windowed Encoding Complexity of SC-LDGM Codes for Lossy Source Compression,” Proc. International Symposium on Information Theory and Its Applications, Monterey, CA, Oct. 2016.
  • A. Golmohammadi* and D. G. M. Mitchell, “Concatenated Spatially Coupled LDPC Codes for Joint Source Channel Coding,” Proc. IEEE International Symposium on Information Theory, pp. 631-635, Vail, CO, June 2018.
  • A. Golmohammadi, D. G. M. Mitchell, J. Kliewer, and D. J. Costello, Jr., “Windowed Encoding of Spatially Coupled LDGM Codes for Lossy Source Compression,” Proc. IEEE International Symposium on Information Theory, Barcelona, Spain, July 2016.

Generalized Codes for Ultra-reliable Low-Latency Communication

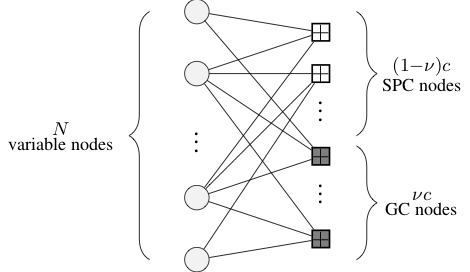Fifth-generation (5G) systems aim to increase the capacity of existing mobile networks by a factor of 1000, supporting an extremely high user density, as well as numerous device-to-device and machine communications. Ultra Reliable Low Latency Communication (URLLC) constitutes one of the critical operating regimes in 5G, since it will enable low-cost and power-efficient anywhere and anytime signalling services. Generalized low-density parity-check (GLDPC) codes, where single parity-check (SPC) constraints on the code bits are replaced with generalized constraints (an arbitrary linear code), are a promising class of codes for URLLC. In this project, a practical construction of quasi-cyclic (QC) GLDPC codes is proposed, where the proportion of generalized constraints is determined by an asymptotic analysis. The block error rate (BLER) performance of the GLDPC codes, combined with a complementary outer code, is shown to outperform a variety of state-of-the-art code and decoder designs with suitable lengths and rates for the 5G URLLC regime.

Selected publications:

  • P. M. Olmos, Y. Liu*, and D. G. M. Mitchell, "Low-density Parity-check (LDPC) Codes for 5G Communications," Wiley 5G Ref: The Essential 5G Reference Online (eds. R. Tafazolli, C.‐L. Wang and P. Chatzimisios), Wiley & Sons, Jan. 2021.
  • Y. Liu*, P. M. Olmos, and D. G. M. Mitchell, "Generalized LDPC codes for Ultra Reliable Low Latency Communication in 5G and Beyond," IEEE Access, Special Issue on Advances in Channel Coding for 5G and Beyond, vol. 6, no. 1, pp. 72002-72014, Dec. 2018.
  • S. Habib* and D. G. M. Mitchell, "Reinforcement Learning for Sequential Decoding of Generalized LDPC Codes," Proc. International Symposium on Topics in Coding, pp. 1-5, Brest, France, Sept. 2023.
  • R. Smarandache and D. G. M. Mitchell, “A Unifying Framework to Construct QC-LDPC Tanner Graphs of Desired Girth,” IEEE Transactions on Information Theory, vol. 68, no. 9, pp. 5802-5822, Sept. 2022.

Low-Complexity Hardware Implementation of Codes

Quasi-cyclic (QC) low-density parity-check (LDPC) codes are of great interest to code designers, since they can be encoded with low complexity using simple feedback shift-registers and their structure leads to efficiencies in decoder design. Moreover, QC codes can be shown to perform well compared to random codes for moderate block lengths. The conventional algorithms for decoding LDPC codes rely on (various forms of) the belief-propagation (BP) algorithm and involve iterative message-passing (MP) on the code’s bipartite Tanner graph, consisting of check nodes and variable nodes. In a hardware implementation of any MP algorithm, messages are inevitably quantized, i.e., represented with a fixed number of bits. As a result, a practical implementation may experience performance that is inferior to models in which quantization is not considered.

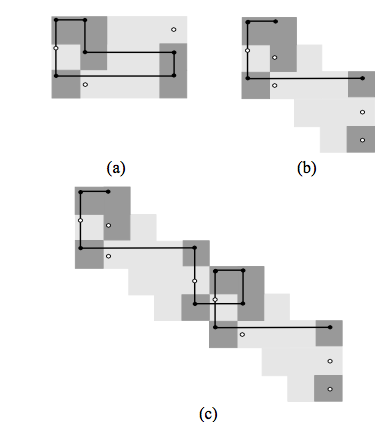
Some of the results published in this project include: 1) A code-independent performance bound for quantized low-density parity-check (LDPC) decoders; 2) a method for constructing QC-LDPC codes using a two-step lifting procedure based on a protograph, that results in provably improved minimum distance and girth properties; and 3) techniques to construct high-rate efficiently encodable LDPC codes with improved optimized absorbing set spectrum by “breaking” problematic substructures (see figure on right).

Selected publications:

  • H. Hatami, D. G. M. Mitchell, D. J. Costello, Jr., and T. Fuja, “A Threshold-Based Min-Sum Algorithm to Lower the Error Floors of Quantized LDPC Decoders,” IEEE Transactions on Communications, vol. 68, no. 4, pp. 2005-2015, Apr. 2020.
  • H. Hatami, D. G. M. Mitchell, D. J. Costello, Jr., and T. Fuja, “Performance Bounds and Estimates for Quantized LDPC Decoders,” IEEE Transactions on Communications, vol. 68, no. 2, pp. 683-696, Feb. 2020.
  • H. Hatami, D. G. M. Mitchell, D. J. Costello, Jr., and T. E. Fuja, "Threshold-based min-sum algorithm to lower the error floors of quantized low-density parity-check decoders," U.S. Patent No. 12,334,954 B1, issued June 17, 2025.
  • D. G. M. Mitchell, R. Smarandache, and D. J. Costello, Jr., “Quasi-Cyclic LDPC Codes Based on Pre-lifted Protographs,” IEEE Transactions on Information Theory, vol. 60, no. 10, pp. 5856-5874, Oct. 2014.

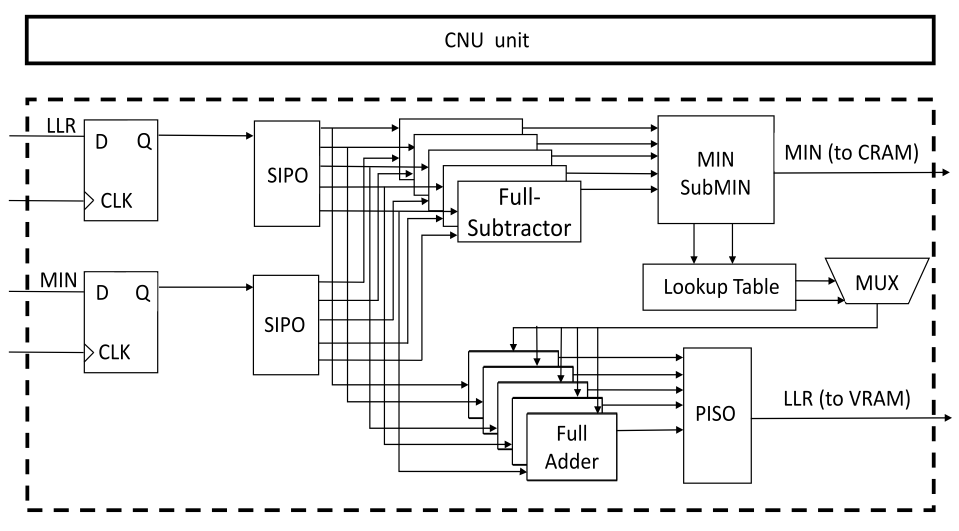We have also developed hardware realizations of LDPC decoders and encoders, including: 1) decoders with a novel lookup table based threshold attenuation technique, called threshold attenuated MSA (TAMSA). The TAMSA implementation was shown to improve bit error rate performance compared to conventional methods with no extra circuit power or circuit area compared to conventional AMSA, and only 0.07% extra leaf cells compared to conventional MSA; and 2) hardware-friendly LDPC encoder circuits for improved arrhythmia detection. These ternary LDPC codes significantly improve classification accuracy in the presence of errors. For example, with an error probability of up to 21% in the sensor output bitstreams, the classification accuracy remains above 99% with the proposed system.

  • D. G. M. Mitchell and Y. Liu*, "Efficient Implementation of a Threshold Modified Min-Sum Algorithm for Low-Density Parity-Check Decoders," U.S. Patent No. 11,309,915, issued April 2022.
  • Y. Liu*, X. Tang, D. G. M. Mitchell, and W. Tang, "Ternary LDPC Error Correction for Arrhythmia Classification in Wireless Wearable Electrocardiogram Sensors," IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 69, no. 1, pp. 38-400, Jan. 2022.
  • Y. Liu*, W. Tang, and D. G. M. Mitchell, "Efficient Implementation of a Threshold Modified Min-Sum Algorithm for LDPC Decoders," IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 67, no. 9, pp. 1599-1603, Sept. 2020.

Robust Error Control for Time-Varying Channels

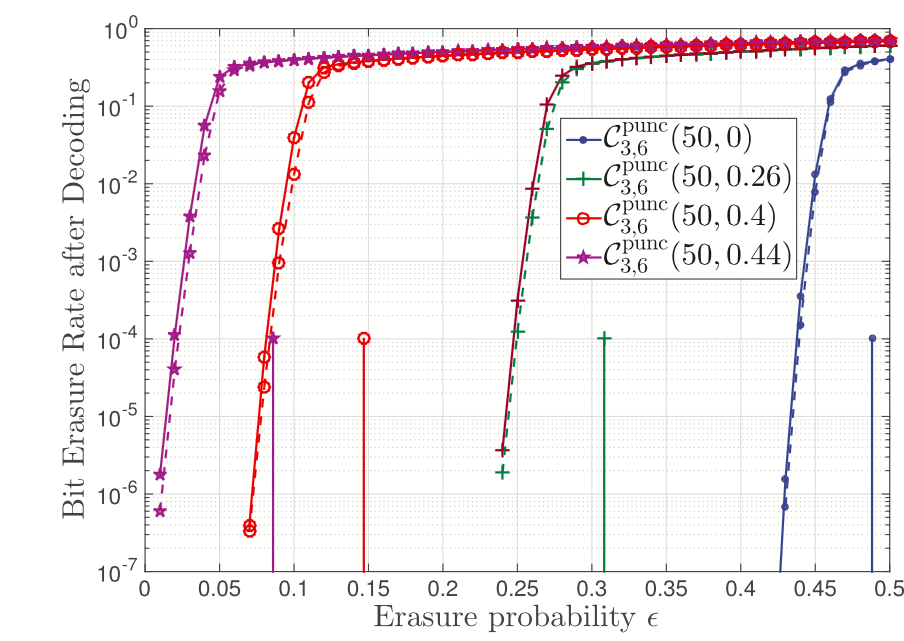It is often desirable in applications that experience changing channel conditions to be able to employ a variety of code rates with the same decoding hardware. One method to achieve this is to puncture a low rate mother code. In this scheme, the transmitter punctures coded symbols, and, as a result of having fewer transmitted code symbols, the code rate is increased. Coding schemes that use this technique are known as rate-compatible punctured codes.

In this project, we perform a random puncturing analysis of low-density parity-check (LDPC) code ensembles, deriving a simple analytic expression for the iterative belief propagation (BP) decoding threshold of a randomly punctured LDPC code ensemble on the binary erasure channel (BEC) and show that, with respect to the BP threshold, the strength and suitability of an LDPC code ensemble for random puncturing is completely determined by a single constant. We also construct codes that show remarkably robust performance over a variety of coding rates (see the figure on the right).

Selected publications:

  • D. G. M. Mitchell, M. Lentmaier, A. E. Pusane, and D. J. Costello, Jr., “Randomly Punctured LDPC Codes,” IEEE Journal on Selected Areas in Communications, vol. 34, no. 2, pp. 408-421, Feb. 2016.
  • A. D. Cummins*, D. G. M. Mitchell, and E. Perrins, “Rate-Compatible, Bandwidth-Efficient, Low-Density Parity-Check (LDPC) Codes for Aeronautical Telemetry,” Entropy, Special Issue on Coding for Aeronautical Telemetry, vol. 26, no. 12: 1o45, pp. 1-17, Dec. 2024.
  • H. Zhou, D. G. M. Mitchell, N. Goertz, and D. J. Costello, Jr., “Robust Rate-Compatible Punctured LDPC Convolutional Codes,” IEEE Transactions on Communications, vol. 61, no. 11, pp. 4428-4439, Nov. 2013.
  • H. Zhou, D. G. M. Mitchell, N. Goertz, and D. J. Costello Jr., “A Puncturing Algorithm for Rate-Compatible LDPC Convolutional Codes”, winner of best student paper, Proc. International Symposium on Turbo Codes and Iterative Information Processing, Gothenburg, Sweden, Aug. 2012.

High-rate Coupled Turbo/LDPC Codes for Optical/Streaming Applications

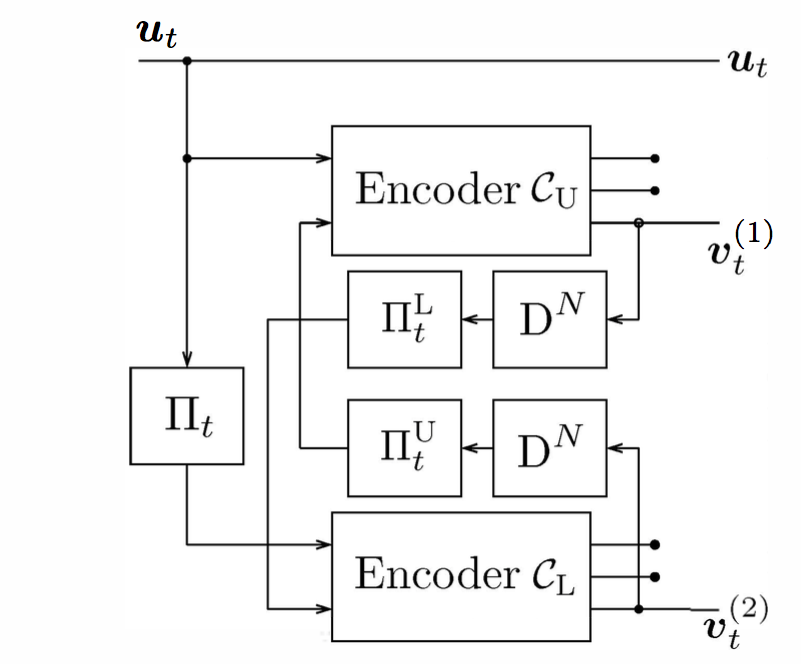Braided convolutional codes (BCCs) are a type of parallel-concatenated convolutional code in which the parity outputs of one component encoder are fed back and used as inputs to the other component encoder at the succeeding time unit (see the figure on the right). Blockwise BCCs have the advantage that both the encoding and decoding can be performed in a fashion similar to turbo codes for which efficient hardware implementations exist. Based on their excellent performance in both the waterfall and error-floor regions, the robustness of this performance to puncturing, and the ability to employ a low-complexity soft decision decoding algorithm at high code rates, blockwise BCC codes appear to be worthy competitors to the product-like codes that have recently been proposed for high-speed optical communication.

Selected publications:

  • M. Zhu, D. G. M. Mitchell, M. Lentmaier, and D. J. Costello, Jr., "Error Propagation Mitigation in Sliding Window Decoding of Braided Convolutional Codes," IEEE Transactions on Communications, vol. 68, no. 11, pp. 6683-6698, Nov. 2020.
  • M. Zhu, D. G. M. Mitchell, M. Lentmaier, D. J. Costello, Jr., and B. Bai, “Braided Convolutional Codes with Sliding Window Decoding,” IEEE Transactions on Communications, vol. 65, no. 9, pp. 3645-3658, Sept. 2017.
  • D. J. Costello, Jr., M. Lentmaier, and D. G. M. Mitchell, “New Perspectives on Braided Convolutional Codes,” Proc. International Symposium on Turbo Codes and Iterative Information Processing, Brest, France, Sept. 2016.
  • D. G. M. Mitchell, A. E. Pusane, M. Lentmaier, and D. J. Costello, Jr., “On the Block Error Rate Performance of Spatially Coupled LDPC Codes for Streaming Applications,” Proc. IEEE Information Theory Workshop, Cambridge, UK, Sept. 2016.
  • M. Zhu, D. G. M. Mitchell, M. Lentmaier, D. J. Costello, Jr., and B. Bai, “Window Decoding of Braided Convolutional Codes”, Proc. IEEE Information Theory Workshop, Jeju Island, Korea, Oct. 2015.

Acknowledgements

The material described above is based upon work supported in part by the National Science Foundation under Grant Nos. CCF-2145917, CCSS-1710920, CCF-1161754, OIA-1757207, and HRD-1914635, and in part by the National Aeronautics and Space Administration (NASA) Training Grant NNX15AL51H.